There has been a proliferation of data vendors selling to investment managers in recent years. And where a select group of systematic or quantitative fund managers were once the vendors’ primary customers, much of the asset management industry is now taking a closer look.

Vendors offer a wide range of datasets, from shipments of commodities around the world to forecasts of crop yields derived from satellite images. Other vendors offer data that contains sensitive personal information, such as credit card records or location data.

Sensitive data of this kind is of interest to asset managers because it can potentially be analysed to reveal consumer spending trends and patterns. But it is the broad trends themselves, rather than the specific information on individuals, that may contain useful insights for financial market investment.

In fields other than finance, there are other legitimate uses of sensitive data that may benefit the public. Urban planning could be enhanced by data revealing trends in the movement of people, as shown in this research involving ride-sharing firm Uber. Nonetheless, there is a significant risk that some of the data on sale could be misused. For this reason, Winton has a policy of not acquiring data that could be interrogated to identify private individuals without their consent.

Gaining confidence in a technique that simultaneously protected people’s privacy while preserving overarching patterns in a given dataset might be one reason to revisit this policy. To that end, we launched a differential privacy study with leading academics in privacy protection at the University of California, Berkeley.

Traditional Approaches to Protecting Privacy

Companies are generally aware of their regulatory and moral obligations to protect people’s privacy when using datasets, and most make good faith efforts to do so. One typical measure is to remove personally identifiable information (PII) from the data in question. The table that follows below provides a stylized example: names have been removed, zip codes obscured and ages bucketed into ranges.

This is a naive approach, however, which often does little to prevent identification. In this case, even after removing obviously sensitive information, such as names and addresses, it may still be possible to deduce individual identities. In fact, with just basic information, including ZIP codes, gender, age, or road vehicle models, the possible identity of a person can often be narrowed down to a small group.

Even if the data itself contains insufficient information to reveal someone’s identity, that data can still sometimes be combined with additional datasets to expose sensitive details. This is not simply a theoretical concern. In 2014, city officials in New York released an anonymized yet public dataset of taxi rides in the city. By cross-referencing the data with photographs of celebrities taking taxi rides that were published on celebrity gossip sites, it was possible to match their identities to the corresponding trips in the data. Ultimately, analysis reveal detailed information on the destinations chosen and fares paid for several well-known celebrities.

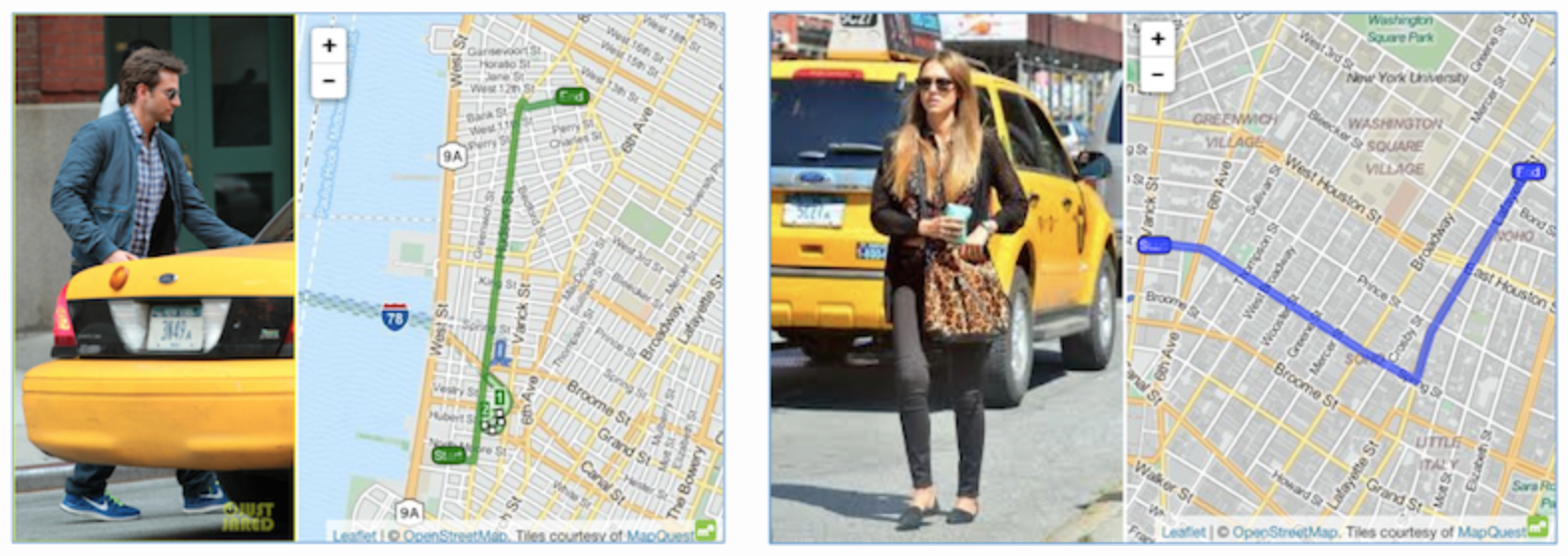
Other information to have been de-anonymized in the past includes medical records, movie preferences and individuals' search engine queries.

And while slightly more sophisticated approaches to anonymization exist, including k-anonymity, all the traditional approaches have been shown to be vulnerable to privacy being compromised.

Differential Privacy

Differential privacy takes a different tack. It starts from the principle that adding any one person’s individual data to a dataset should not materially change the result of queries run on that data. This broadly corresponds to people’s intuitive notion of privacy - namely, that their data should not be able to be singled out by specific queries.

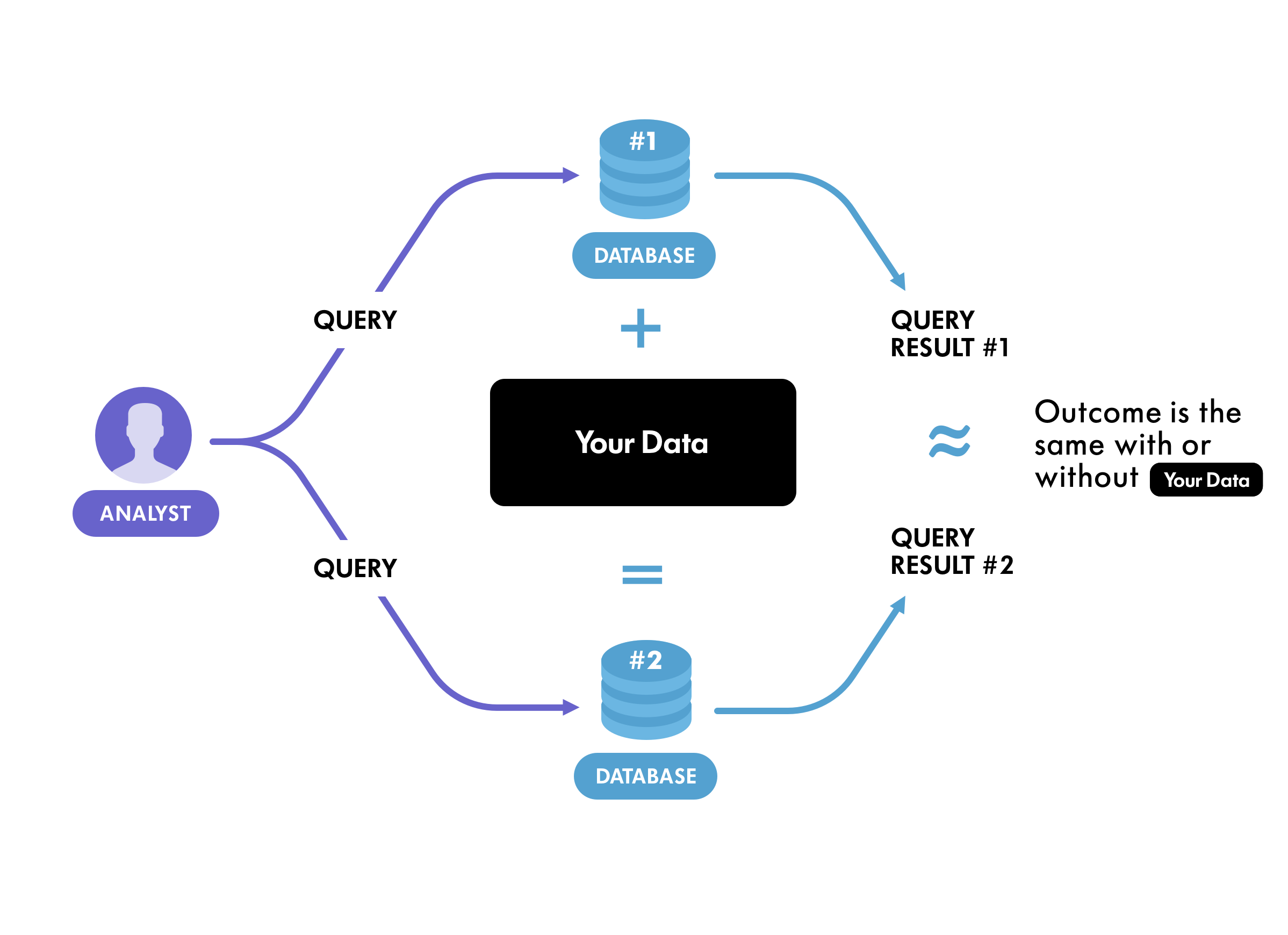
The mechanism used by differential privacy to protect privacy is to add noise to data purposefully (deliberate errors, in other words) so that even if it were possible to recover data about an individual, there would be no way to know whether that information was meaningful or nonsensical. One useful feature of this approach is that even though errors are deliberately introduced into the data, the errors roughly cancel each other out when the data is aggregated.

Consider a case where the information required is the number of people to have visited a park. Differential privacy could produce an approximate count that would be useful for urban planning purposes. The data on any single individual, however, would not be reliable enough to indicate whether they had been present at a given time.

Several online resources give useful overviews on the subject of differential privacy, such as a two-part overview by Neustar. Part 1 of this overview explains the basic concepts, while part 2 uses the New York Taxi data highlighted above to demonstrate how differential privacy protects individuals' information, while preserving high-level trends and patterns in data that can be used by city officials for making better data-driven urban planning decisions.

Differential privacy operates via a solid underlying mathematical framework based on probability and statistics. When queries are simple counts, the type of noise usually added to data is derived from a probability distribution called the Laplace distribution. The Laplace distribution has a parameter that is proportional to the standard deviation of the distribution and which controls how “noisy” it is.

For a given privacy budget, which determines how many times a dataset can be queried before starting to leak information, there is a provably correct mathematical formula that determines the parameter setting for the Laplace distribution parameter. This is usually referred to as epsilon ε.

Epsilon therefore gives a mathematically sound dial to control the trade-off between privacy and usefulness. The rigorous mathematical foundation for differential privacy stands in marked contrast to some of the ad hoc heuristics that have been used previously to protect individual privacy.

To pursue this approach further, John Funge from Winton’s San Francisco team contacted a group of researchers led by Professor Dawn Song at UC Berkeley. Professor Song’s group had already conducted research with Uber, with the latter leading to the release of an open source differential privacy project. The open source project implements differential privacy with a query analysis and rewriting framework that takes certain classes of queries and then re-writes the queries. The queries are written in SQL, the industry-standard query language.

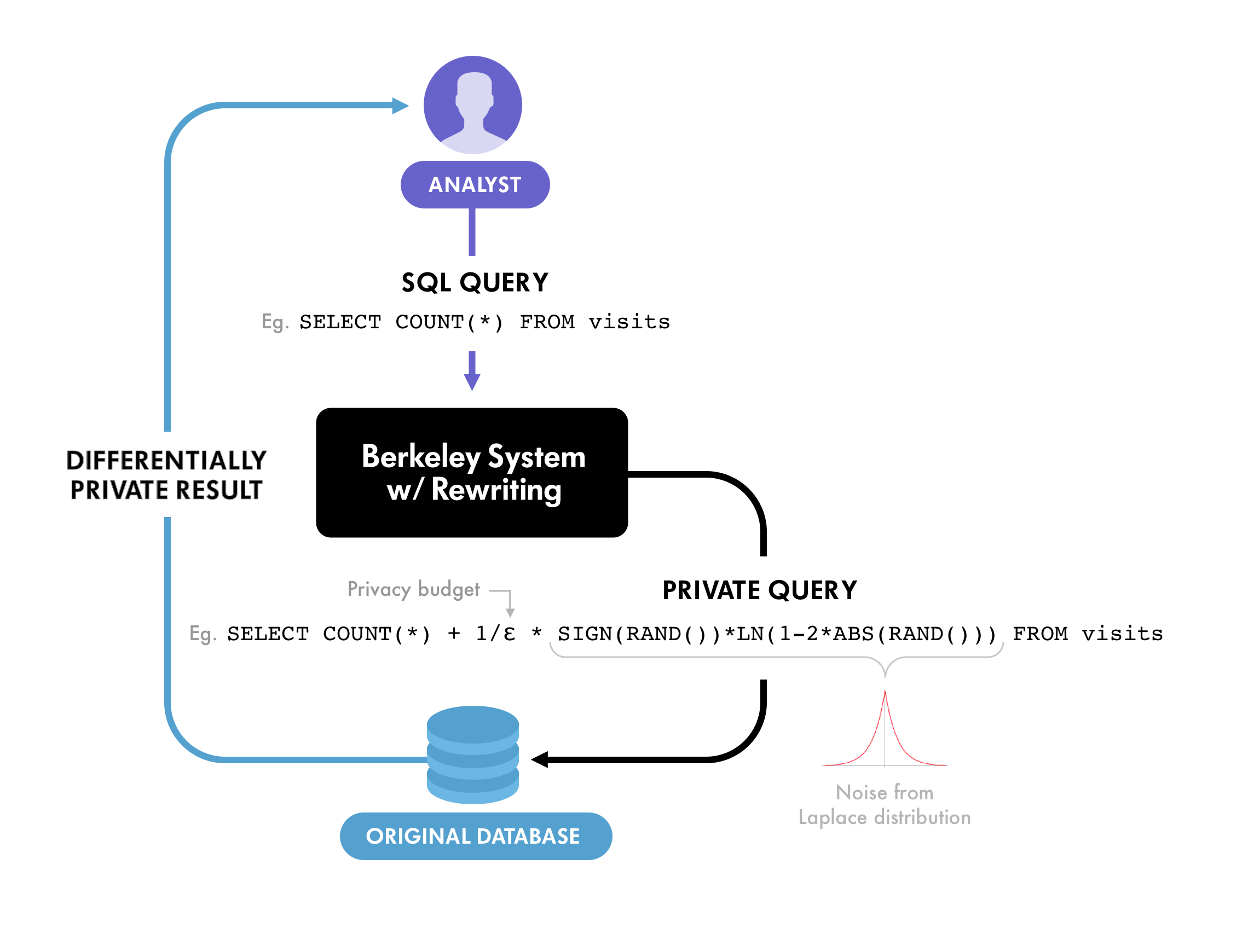
The query re-writing involves adding noise such that the results, returned as the response, protect privacy. This is the framework used in the examples below, which should clarify how differential privacy might be used in the context of investment management.

Location Data

As a proof of concept, we chose to look at certain location data provided by a third-party data vendor. Even though it was a research project, we had no desire to store such sensitive data on Winton’s own infrastructure.

The attraction of differential privacy is that such storage is not a requirement. Researchers at Winton could write SQL database queries for macro-scale trends in the data, and the queries could then be converted to differentially private versions using the technology provided by the Berkeley researchers.

The transformed and differentially-private version of the queries would then run on a database hosted by the data provider and the privacy-preserved results would be returned to Winton.

This is best explained with an example. Suppose we are interested in the relative performance of two big-box rival retailers: Home Depot (abbreviated below to “HD”) and Lowe's. Given data on many individuals' locations, one can then count how many of those people visit stores owned by the two companies. By looking at this data over time and in different regions, it is in theory possible to identify patterns and trends that might be useful in generating close to real-time forecasts of sales. If we observed a falling number of shoppers at Lowe's, it might be possible to draw a link to the company's recent store closures at its Orchard subsidiary.

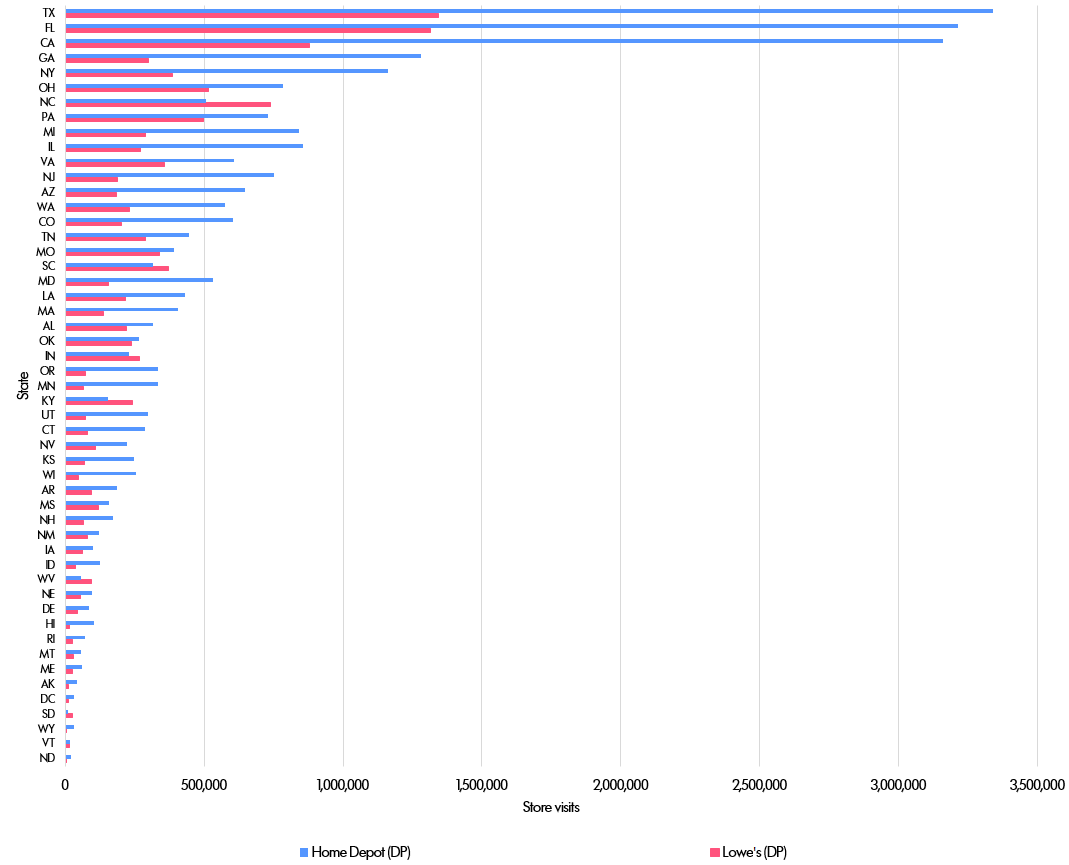
The first step was simply to count the aggregate number of monthly store visits by US state.

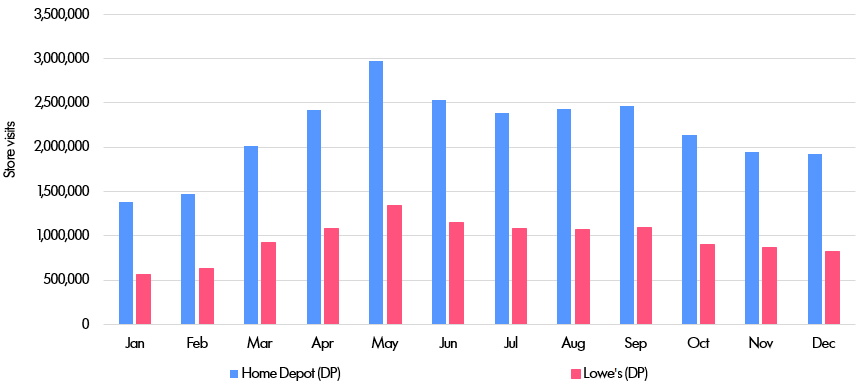
And here is the graph of visits by state.

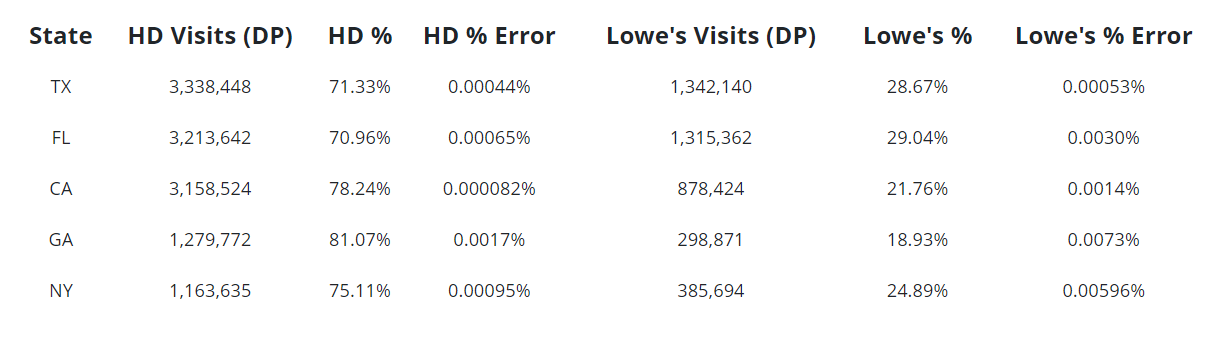
Closer analysis of the data for the five states with the most visits reveals the amount of error produced by differential privacy (DP). The errors are a result of the noise deliberately added to the data, but for large numbers such as these the amount of noise is so small as to leave intact broader trends in the data.

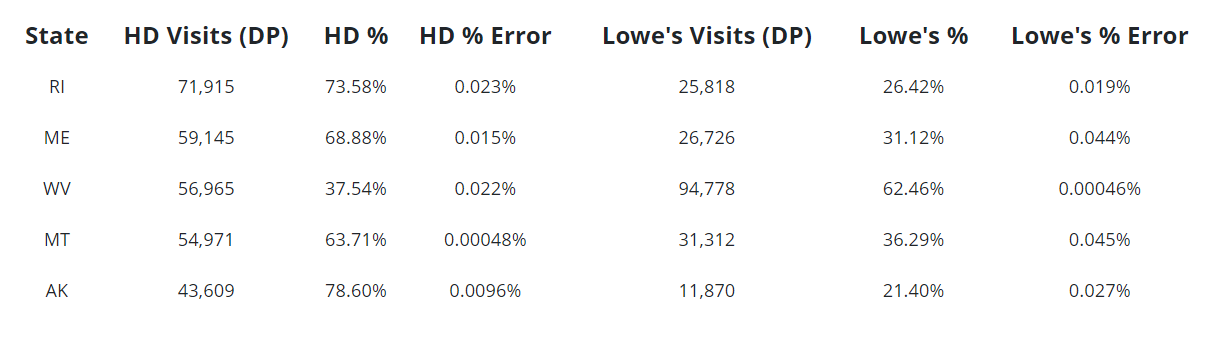
Now if we look at the five states with the lowest counts, we can see that the error rates due to differential privacy are much higher, as we might expect. Yet they are still low enough such that any material conclusions from the analysis should be robust.

Next, consider a query that might threaten privacy, such as an analyst attempting to look at data at the zip code level. As the table below shows, the error rates soar. This is on account of the raw counts being extremely low, which necessitates high error rates being introduced. The result is that these high error rates protect potentially sensitive information.

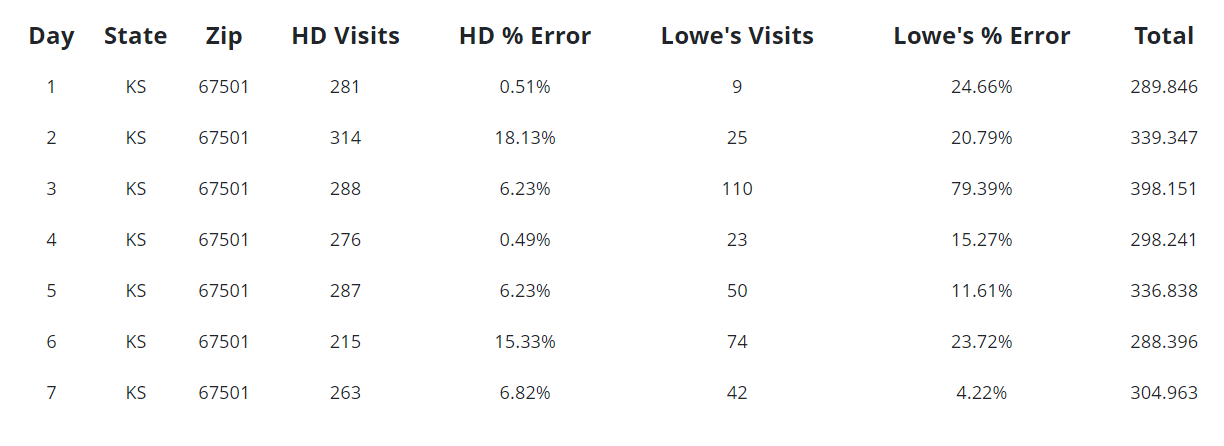
Note that in an actual differential privacy production system, error rates would never be provided in such fine detail. Instead, analysts who executed a privacy-threatening query would just receive unusable noise, thus protecting privacy.

It is easier to grasp this visually with the errors displayed as error bars. To reiterate, these error breakdowns are for illustrative purposes and would not be provided to the user. Indeed, a typical user's experience would be that the privacy-threatening results would be entirely useless, given the scale of the errors that had been introduced.

Illustrative noise (error) introduced by differential privacy for daily store visits for a specific zip code in KS.

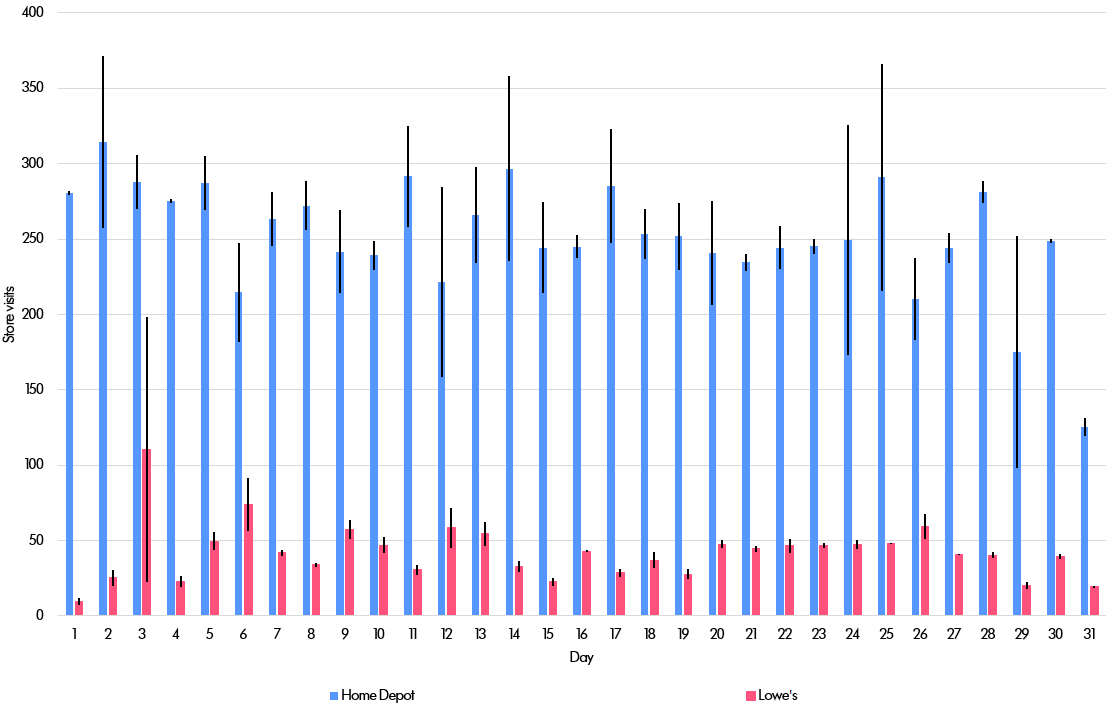
Finally, imagine a much more complicated query that involves joining data together across more than one database table. Suppose we wanted to see how many people visit Home Depot first and Lowe’s second on the same day (and vice versa). That involves extracting data from the Home Depot table and then combining that with data from the Lowe’s table to search for people in each table on a certain day. This might be interesting because it could suggest that people fail to find their sought-for goods in the first store visited. It turns out the number of people who visit one store and then follow that up with a visit to the second store is so small that it is difficult to derive a useful result.

The researchers at Berkeley, however, were able to adjust the epsilon parameter controlling the trade-off between accuracy and privacy to produce meaningful results. Here are the results for the whole of the United States. The errors are still low enough to be useful and the privacy guarantees are still very strict. In particular, the epsilon value is 1.0 (higher and therefore less private than the 0.1 that we used for the other results), but still lower than industry standards (according to this article, Apple uses epsilon = 8 for some data and epsilon = 4 for other data, while Google often uses a value around 2).

The Berkeley researchers observed that most of the error comes from the bias introduced by the use of thresholds and not from the noise itself. Eliminating this bias would possibly require new research as it is not something that has likely been considered carefully in the existing literature.

Next Steps

Winton has no plans to start using data derived from location information in its investment algorithms, but differential privacy does give us the technology to safely handle personally sensitive information if at a later date we decide to investigate such data. Just as importantly, the current work shows that for firms of all types interested in the application of such data, there are techniques that can be used to gain insights without compromising privacy.

It is also interesting to note that startups like Oasis Labs, founded by the researchers at Berkeley, are creating privacy-first cloud computing platforms. These platforms will potentially allow investment management firms to run trading algorithms on data provided by data vendors, such that the data vendor never sees the trading algorithm, while the investment manager never sees the data.

Developing and debugging algorithms that run on unseen data will take some time, but there is clear potential to gain insights from sensitive datasets while protecting individual privacy. Winton and Berkeley’s research has shown that differential privacy is a promising area for future work.